Tato část je uvedena spíš pro informaci o tom, jak řešit integraci racionální lomené funkce. Zájemci o tuto problematiku najdou vše podrobněji ve vysokoškolských učebnicích integrálního počtu.
Racionální lomená funkce proměnné x je funkce tvaru
![]()
kde S(x) a Q(x) jsou mnohočleny, přičemž Q(x) je stupně aspoň prvého a dělení
![]()
nevyjde beze zbytku.
Je definována pro všechna x, kromě těch, pro něž je Q(x) = 0.
Je-li dána racionální lomená funkce
![]()
a je-li mnohočlen S(x) stupně m, Q(x) mnohočlen stupně n > 0 a je-li m ≥ n, lze dělením převést funkci
![]()
na tvar
![]()
kde P(x) je nižšího stupně než Q(x).
Např. je-li
![]()
lze po vydělení tuto funkci převést na tvar
![]()
Je tedy v tomto případě
![]()
Budeme nyní předpokládat, že
![]()
je taková racionální lomená funkce, kde je stupeň čitatele P(x) menší než stupeň jmenovatele Q(x).
Omezíme se však jen na dva nejjednodušší typy racionálních funkcí lomených, kdy jmenovatel Q(x) je prvního nebo druhého stupně, tj. integrály tvaru
![]()
kde a, b, c, m, n jsou konstanty, přičemž a ≠ 0.
První integrál lze řešit substitucí t = ax + b, potom dt = a dx,
![]()
Druhý integrál
![]()
může být trojí:
a) Jmenovatel ax2 + bx + c lze rozložit v součin dvou různých lineárních dvojčlenů. To nastane tehdy, má-li rovnice ax2 + bx + c = 0 dva různé reálné kořeny x1, x2, čili když diskriminant b2 - 4ac > 0. V tomto případě rozložíme zlomek
![]()
v součet dvou zlomků
![]()
a porovnáním obou zlomků určíme konstanty A, B. Je totiž
![]()
Oba zlomky mají téhož jmenovatele, proto i čitatelé se sobě rovnají. Z toho vyplývá
![]()
Odtud vyplývá
![]()
Daný integrál je pak roven součtu dvou integrálů
![]()
které umíme počítat.
Příklad
Máme vypočítat integrál
![]()
Řešení
Nejprve rozložíme jmenovatele a dostaneme
![]()
![]()
na součet dvou zlomků
![]()
a porovnáním zlomků dostaneme
![]()
neboli
![]()
Sestavíme rovnice pro konstanty A, B:
![]()
Odtud dostáváme
![]()
Daný integrál pak je
![]()
b) Jmenovatel ax2 + bx + c je druhá mocnina nebo násobek druhé mocniny lineárního dvojčlenu. To nastane, má-li rovnice ax2 + bx + c = 0 dvojnásobný kořen
![]()
čili když diskriminant b2 - 4ac = 0. Pak je
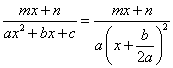
a integrál
![]()
vypočteme substitucí
![]()
Příklad
Vypočtěte
![]()
Řešení
Protože jmenovatel x2 - 4x + 4 = (x - 2)2, je
![]()
Užijeme-li k výpočtu substituce
![]()
dostaneme
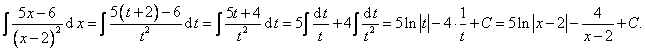
c) Jmenovatel ax2 + bx + c nelze rozložit v součin. To nastane tehdy, nemá-li rovnice ax2 + bx + c = 0 reálné kořeny, čili když diskriminant b2 - 4ac < 0. V tomto případě rozložíme nejprve zlomek
![]()
na dva zlomky tak, aby první obsahoval v čitateli násobek derivace jmenovatele ax2 + bx + c a druhý konstantu. Tedy
![]()
což je možné jen tak, že
![]()
Potom
![]()
Rozklad tedy je
![]()
Nyní můžeme integrovat
![]()
Výpočet integrálu
![]()
si ukážeme na konkrétním příkladu.
Příklad
Vypočtěte integrál
![]()
Řešení
Protože diskriminant 4 - 28 < 0, rozložíme zlomek
![]()
na dva zlomky, z nichž první má v čitateli násobek derivace jmenovatele x2 + 2x + 7 a druhý konstantu. Platí (x2 + 2x + 7)´ = 2x + 2 a proto položíme
![]()
Porovnáním zlomků dostaneme
![]()
Dále je
![]()
První integrál
![]()
Absolutní hodnotu nepíšeme, protože pro každé x je x2 + 2x + 7 > 0.
Pro výpočet druhého integrálu
![]()
upravíme nejprve jmenovatele
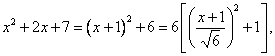
pak zavedeme substituci
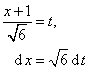
a dostaneme
![]()
Celkem tedy obdržíme
![]()