Základem metody je vzorec pro derivaci součinu, ze kterého je celá tato metoda odvozena.
Budeme předpokládat, že všechny funkce i jejich derivace jsou požadovaných intervalech spojité.
Platí
![]()
Poznámka 1
Odvození lze provést z věty pro derivaci součinu:
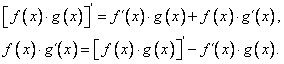
Po integraci posledního řádku dostaneme požadovaný vztah.
Poznámka 2
Častěji se tento vzorec používá ve zkrácené podobě. Označíme-li f(x) = u, g(x) = v, je tato metoda vyjádřena vzorcem
![]()
Poznámka 3
Popsaná integrační metoda vede k cíli, podaří-li se nám v součinu f(x)g´(x) najít takový činitel g´(x), ke kterému snadno určíme ∫g´(x) dx = g(x), umíme-li vypočítat i druhý integrál ∫f ´(x) g(x) dx.
Nyní si ukážeme výše uvedenou metodu na několika příkladech. (Pokud neuvádíme žádné požadavky na x, máme na mysli x z intervalu (-¥; + ¥).)
Příklad 1
Vypočtěte
![]()
Řešení
Položíme
![]()
Dostáváme
![]()
Příklad 2
Vypočtěte
![]()
Řešení
Položíme
![]()
Dostáváme
![]()
Příklad 3
Vypočtěte
![]()
Řešení
Položíme
![]()
Dostáváme
![]()
Integrál
![]()
vypočteme opět metodou per partes tak, že položíme
![]()
Obdržíme
![]()
(Integrační konstantu zde v tomto mezivýpočtu neuvádíme, uvedeme ji až na závěr.)
Celkem tedy je
![]()
Příklad 4
Vypočtěte integrál
![]()
Řešení
Označíme
![]()
Položíme
![]()
Dostaneme
![]()
Je tedy
![]()
Z této rovnice vypočteme
![]()
Poznámka k řešení: výše uvedený integrál I je možno také vypočítat užitím substituce ln x = t.
Další příklady na integraci per partes jsou uvedeny ve Cvičení 4.