[Návrat do menu integrál]

Určení integrační konstanty

    z počátečních podmínek

Příklad 1

Určete funkci, jejíž derivace je x - 3, víte-li, že pro x = 2 je hodnota funkce rovna 9.

Řešení

Příklad 2

Určete funkci, jejíž derivace je 3 + x - 5x² a jejíž hodnota pro x = 6 je - 200.

Řešení

Příklad 3

Řešení

Řešení

Příklad 6

Určete rovnici křivky, která prochází bodem [0; a] a má tu vlastnost, že směrnice tečny v každém jejím bodě je vyjádřena vzorcem

Řešení

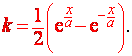
Příklad 7

Těleso se pohybuje rychlostí v, jejíž závislost na čase je vyjádřena rovnicí v = 3t²  + 4t  ms^-1. Za dobu t = 2 s urazí těleso dráhu s = 16 m.  Určete závislost proběhnuté dráhy na čase.

Řešení

Příklad 8

Rychlost v tělesa je dána vzorcem v = 2 cos t ms^-1. Za dobu t = π/4 s urazí těleso dráhu s = 10 m. Určete závislost proběhnuté dráhy na čase.

Řešení

Příklad 9

Zrychlení a tělesa je definováno vzorcem a = t² + 1 ms^-2 . V okamžiku t = 0 s je rychlost v = 1 ms^-1 a dráha s = 0 m. Určete závislost proběhnuté dráhy na čase.

Řešení