Posloupnost je funkce, jejímž definičním oborem je množina N všech přirozených čísel ( nekonečná číselná posloupnost ), je-li definičním oborem množina prvních n přirozených čísel {1, 2, ..., n } jedná se o konečnou posloupnost ( konečnou číselnou posloupnost ) . Funkční hodnoty (konečné nebo nekonečné) se nazývají členy posloupnosti . Funkční hodnota posloupnosti v bodě n Î N se nazývá n - tý člen posloupnosti a značí se místo f(n) zpravidla f n anebo častěji a n , b n .
Posloupnost (nekonečná) s
n - tým členem a n se zapisuje ( a 1 , a 2 , ..., a n , ...) nebo
![]()
Posloupnost konečná s
n - tým členem a n a s definičním oborem {1, 2, ... , k } se zapisuje( a 1 , a 2 , ... , a k ) nebo
![]()
Funkční předpis posloupnosti
![]()
je zpravidla zadán:
Graf posloupnosti je bodový se souřadnicemi bodů [
n, a n ] .
Příklady posloupností zadaných pomocí vzorce pro
n - tý člen:
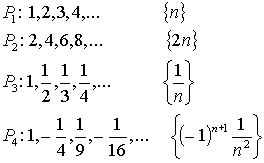
Příklady posloupností zadaných rekurentně (vpravo je vypsáno prvních 5 členů dané posloupnosti):
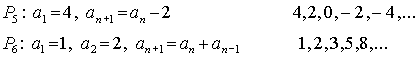
Vlastnosti posloupností
Posloupnost
![]()
se nazývá
shora omezená posloupnost , existuje-li takové číslo h Î R , tak, že
![]()
pro každé
n Î N ,zdola omezená posloupnost , existuje-li takové číslo d Î R , že
![]()
pro každé
n Î N ,
omezená posloupnost , je-li omezená shora i zdola.
Posloupnost
![]()
se nazývá
rostoucí posloupnost , je-li a n+1 > a n pro každé n Î N ,
klesající posloupnost , je-li a n+1 < a n pro každé n Î N ,
nerostoucí posloupnost , je-li a n ³ a n+1 pro každé n Î N ,
neklesající posloupnost , je-li a n+1 ³ a n pro každé n Î N .
Rostoucí, klesající, neklesající, nerostoucí posloupnosti se nazývají monotónní posloupnosti .
Posloupnosti rostoucí a klesající se nazývají ryze monotónní posloupnosti .