[Návrat na hlavní stránku]
Rekurentní vzorec
popisuje, jak je možno posloupnost vytvořit. Plyne z něho základní vlastnost
tj. rozdíl dvou sousedních členů je konstantní.
Vzorec pro a n :
Vztah mezi dvěma členy:
Součet prvních
n členů:
nebo
Ze vzorců pro
a n i s n plyne, že obě tato čísla jsou určena, známe-li čísla a 1 a d .
Rekurentní vzorec
udává, jak je možno posloupnost vytvořit. Ze vzorce plyne vlastnost
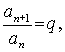
tj. podíl dvou sousedních členů je konstantní.
Vzorec pro a n :
Vztah dvou členů
Součet prvních n členů
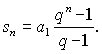
U geometrické posloupnosti je a n exponenciální funkcí svého indexu a čísla a n a s n jsou určena, známe-li čísla a 1 , q .
Budeme-li sčítat u geometrické posloupnosti nekonečný počet členů, tj.
n ® ¥ , a bude-li
dostaneme vztah pro součet
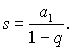
K tomuto vztahu je možno přejít na základě výpočtu pomocí limity. Bude-li splněna podmínka pro q, obdržíme
po dosazení do vztahu pro s n dostaneme výše uvedený vztah pro s .