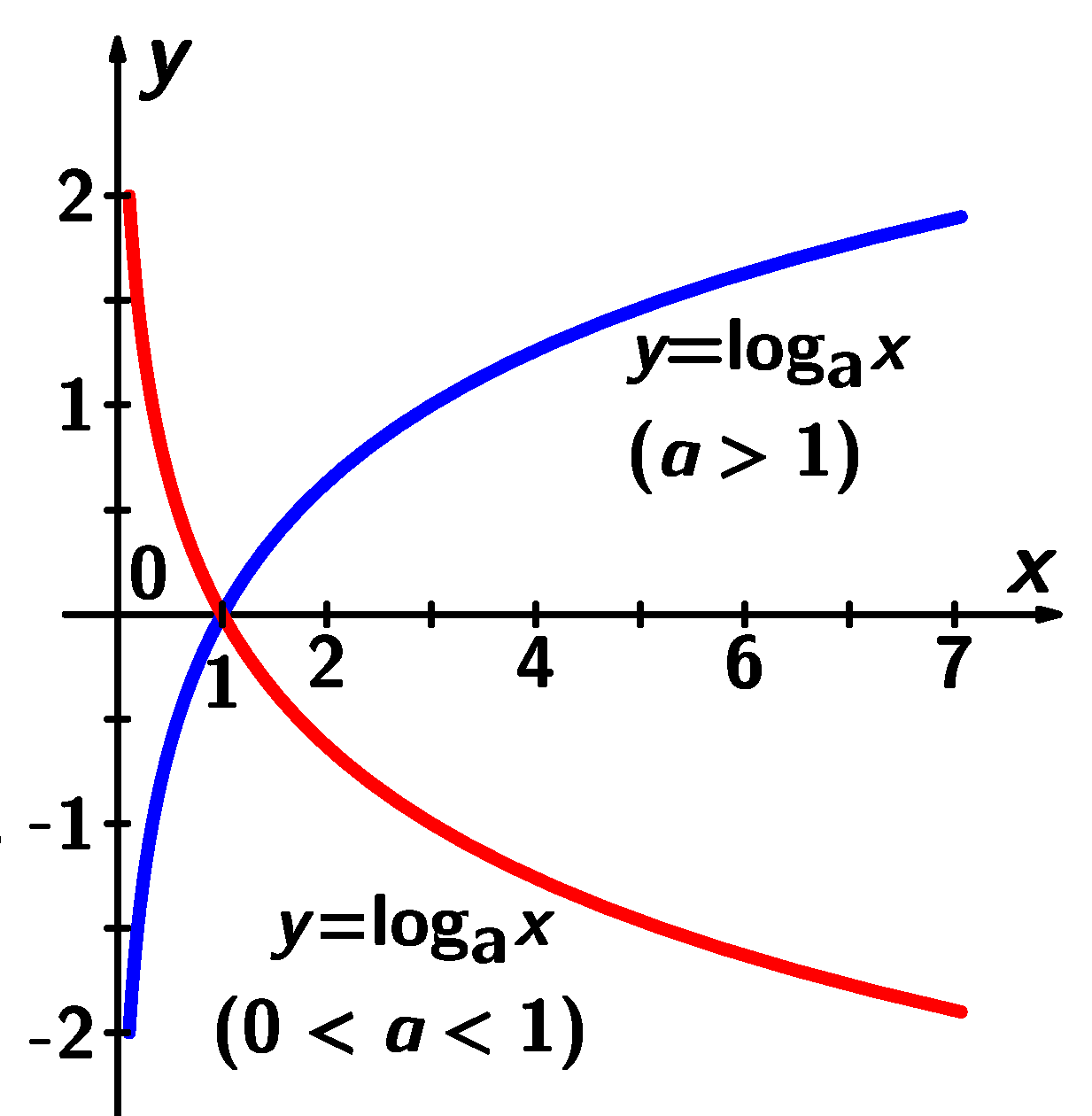
Logaritmická funkce

Matematický popis funkce, základní početní vztahy

Logaritmická funkce o základu a

je funkce inverzní k exponenciální funkci o témž základu a , která je ryze monotónní v definičním oboru R a nabývá v něm všech kladných funkčních hodnot. Definiční obor logaritmické funkce je

Symbolický zápis logaritmické funkce o základu a je

Logaritmická funkce o základu 10, tj. inverzní funkce k dekadické exponenciální funkci, se nazývá dekadická logaritmická funkce .

Logaritmická funkce o základu e, tj. inverzní funkce k přirozené exponenciální funkci, se nazývá přirozená logaritmická funkce, zapisujeme ji ve tvaru

Graf logaritmické funkce je logaritmická křivka . Graf logaritmické funkce o základu a je souměrně sdružený s grafem exponenciální funkce o témže základu a podle přímky o rovnici

Všechny logaritmické křivky procházejí bodem [1; 0] , který je v této souměrnosti obrazem bodu [0; 1] , jímž procházejí všechny exponenciální křivky.