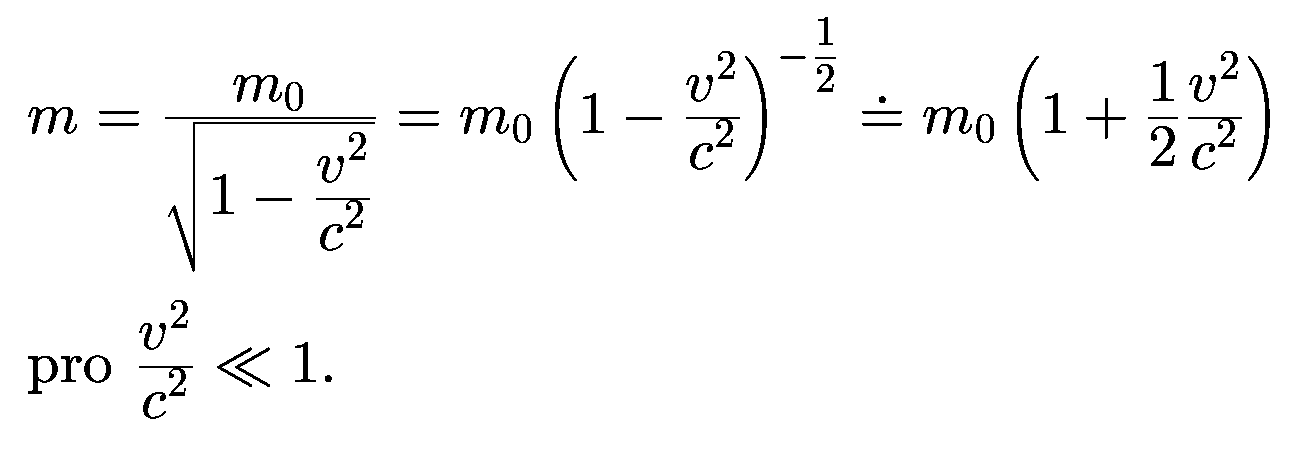Funkci y = f(x) nazýváme v okolí bodu x = x 0 nekonečně malou, je-li
![]()
Budeme uvažovat dvě funkce
g(x) , h(x) nekonečně malé v okolí bodu x 0 . Označíme
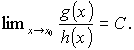
Limita C může mít obecně tyto hodnoty:
Toto můžeme zapsat také tak, že
![]()
pro x ® x 0 .
Řád malosti dané funkce určujeme porovnáním s funkcí
![]()
která je n - tého řádu malosti pro x ® x 0 .
Poznatky z posledního případu používáme ve fyzice, především v případě malých kmitů (ale i např. v geometrické optice a řadě dalších úloh), kdy lze nahradit funkci sin( x ) nebo i tg( x ) hodnotou úhlu v obloukové míře, kdy lze psát
![]()
nebo
![]()
Oba vztahy jsou důsledkem toho, že platí
![]()
Pro x ® 0 můžeme psát
![]()
Naznačíme si důkaz pro
n Î N (Vzhledem k tomu, že tento text je zaměřen na fyzikální aplikace, nebudeme se tímto důkazem podrobněji zabývat. Podrobnější obecný důkaz pro n Î R lze nalézt v učebnicích matematiky.)Ze vztahu uvedeného výše plyne
![]()
Protože pravá i levá strana tohoto vztahu jsou nekonečně malé funkce v okolí bodu
x = 0, stačí dokázat
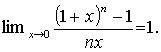
S použitím binomického rozvoje můžeme psát
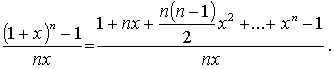
Po tom můžeme psát
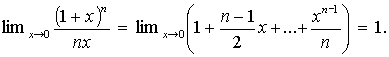
Užití ve fyzice
Při odvození vztahu pro teplotní objemovou roztažnost v případě kvádru (který pak lze zobecnit), známe-li vzorec pro teplotní délkovou roztažnost:
![]()
![]()
objem při teplotě
t pak je
![]()
Při změně objemu kvádru se změní všechny jeho délkové rozměry. Můžeme psát
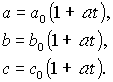
Po dosazení do výše uvedeného vztahu pro objem, dostaneme
![]()
Obdobně bychom mohli dokázat vzorec pro změnu hustoty materiálu v závislosti na teplotě:
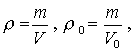
z čehož
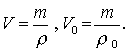
Po dosazení do vzorce pro výpočet objemu dostaneme
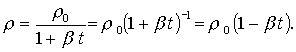
Jiné užití přibližného vzorce
![]()
je v teorii relativity při počítání s odmocninami:
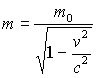
pro
![]()
Platí