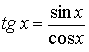
Definice goniometrických funkcí tangens a kotangens:
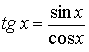
pro každé
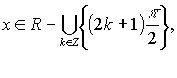
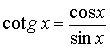
pro každé
![]()
Těmito definičními vztahy je každému přípustnému
x Î R přiřazeno právě jedno reálné číslotg x a právě jedno reálné číslo cotg x , tj. tyto vztahy udávají funkční předpisy funkce tangens
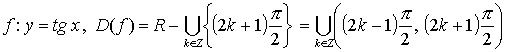
a funkce kotangens
![]()
Grafy funkcí tangens a kotangens lze sestrojit pomocí jednotkové kružnice.
Základní vlastnosti funkcí tangens a kotangens je možno odvodit přímo z definice tg x , cotg x užitím vlastností funkcí sinus a kosinus:
funkce tangens a kotangens jsou liché ve svých definičních oborech
![]()
pro každé
![]()
![]()
pro každé
![]()
(toto plyne ze vztahů
![]()
pro každé
x Î R.)
obě goniometrické funkce
tangens i kotangens jsou periodické se základní periodou p :
![]()
pro každé
![]()
![]()
pro každé
![]()
funkce tangens a kotangens nejsou omezené.
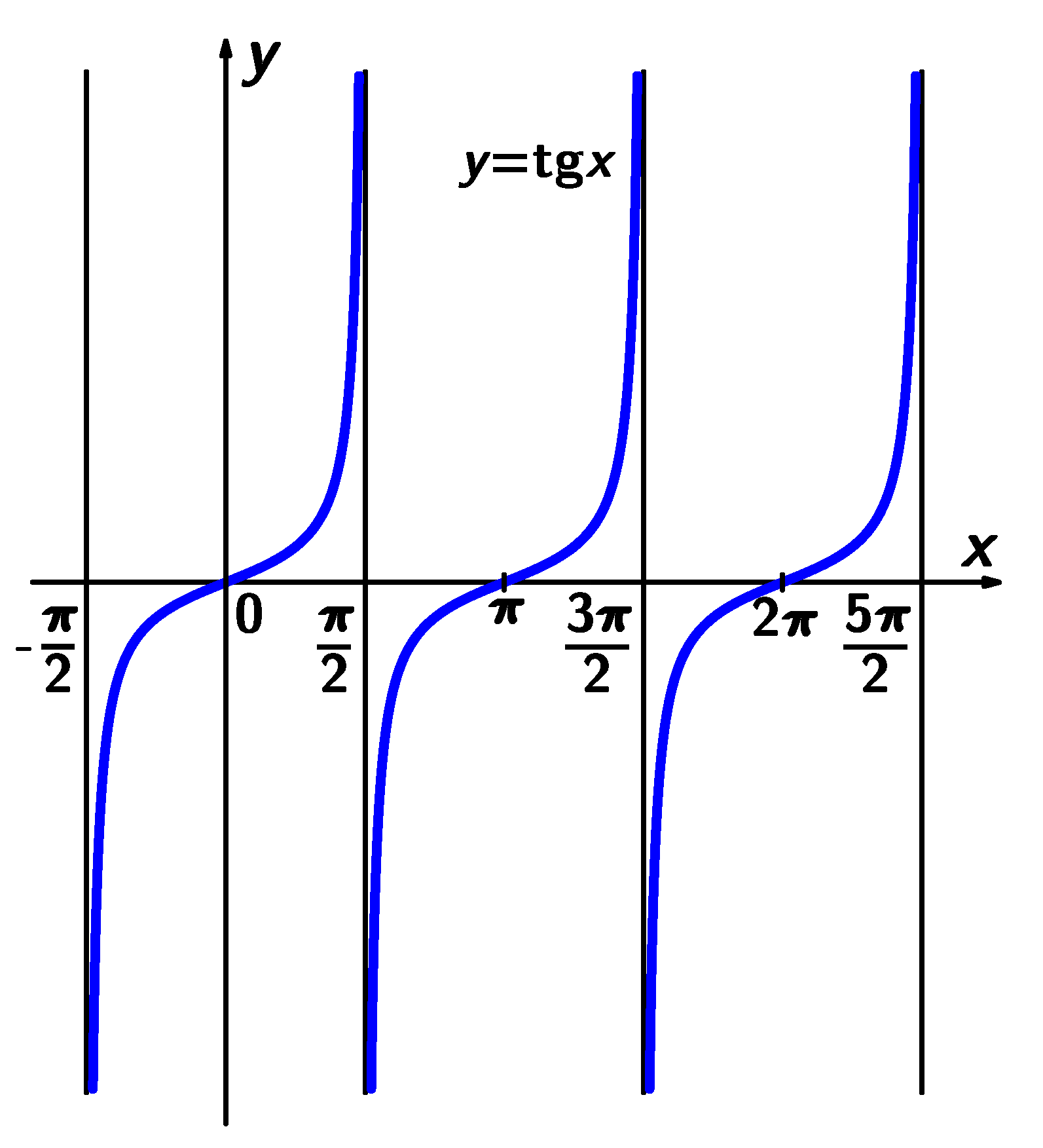
|

|
|---|