[Návrat na hlavní stránku]
a) Budeme uvažovat, že oba kmity mají stejnou periodu, tj.
Potom
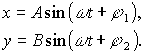
Po úpravě
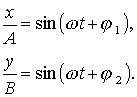
Obě rovnice po řadě vynásobíme činiteli v postranních sloupcích a sečteme je.
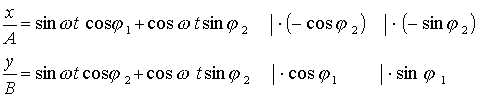
Dostaneme
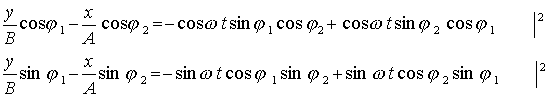
Obě rovnice umocníme na druhou a sečteme, tímto způsobem vyloučíme čas
t :
což je kvadratická rovnice s proměnnými
x , y bez lineárních členů.Nyní budeme diskutovat speciální případy rovnice (1).
1)
Potom
Dostaneme
což je osová rovnice elipsy.
Je-li A = B , dostaneme rovnici kružnice.
2)
z toho vyplývá, že
Platí
nebo
Potom
z čehož
tj.
což jsou rovnice přímek.
b) Bude-li platit:
dostaneme tzv. Lissajousovy obrazce .
Tvar Lissajous ových obrazců závisí také na počáteční fázi j - viz modelování.
Kmity je možno také modelovat .