Skládání více harmonických kmitů ležících v téže přímce. Harmonická analýza.

Před studiem této části je vhodné znát alespoň základy integrálního počtu.

Pro n kmitů můžeme obecně psát:

V obecném případě bude časovým rozvojem takového kmitu složitá neperiodická křivka.

My se však omezíme na případ:

tj. frekvence budou celočíselným násobkem základní frekvence - f _n = n f ₁ - tzv. harmonické frekvence . Výsledný kmit bude složitý, ale periodický.

Opačně také platí: každý periodický pohyb je možno rozložit na součet jednoduchých kmitů s harmonickými frekvencemi - tzv. harmonické složky .

Př. Skládání kmitů:

Obecně je možno psát

Tomuto rozkladu říkáme tzv. harmonická analýza .

k - tý člen lze rozepsat

Nyní položíme

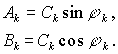
Potom

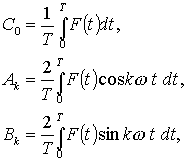
Pro jednotlivé koeficienty pak platí:

kde C ₀ , A _k , B _k jsou tzv. Fourierovy koeficienty .

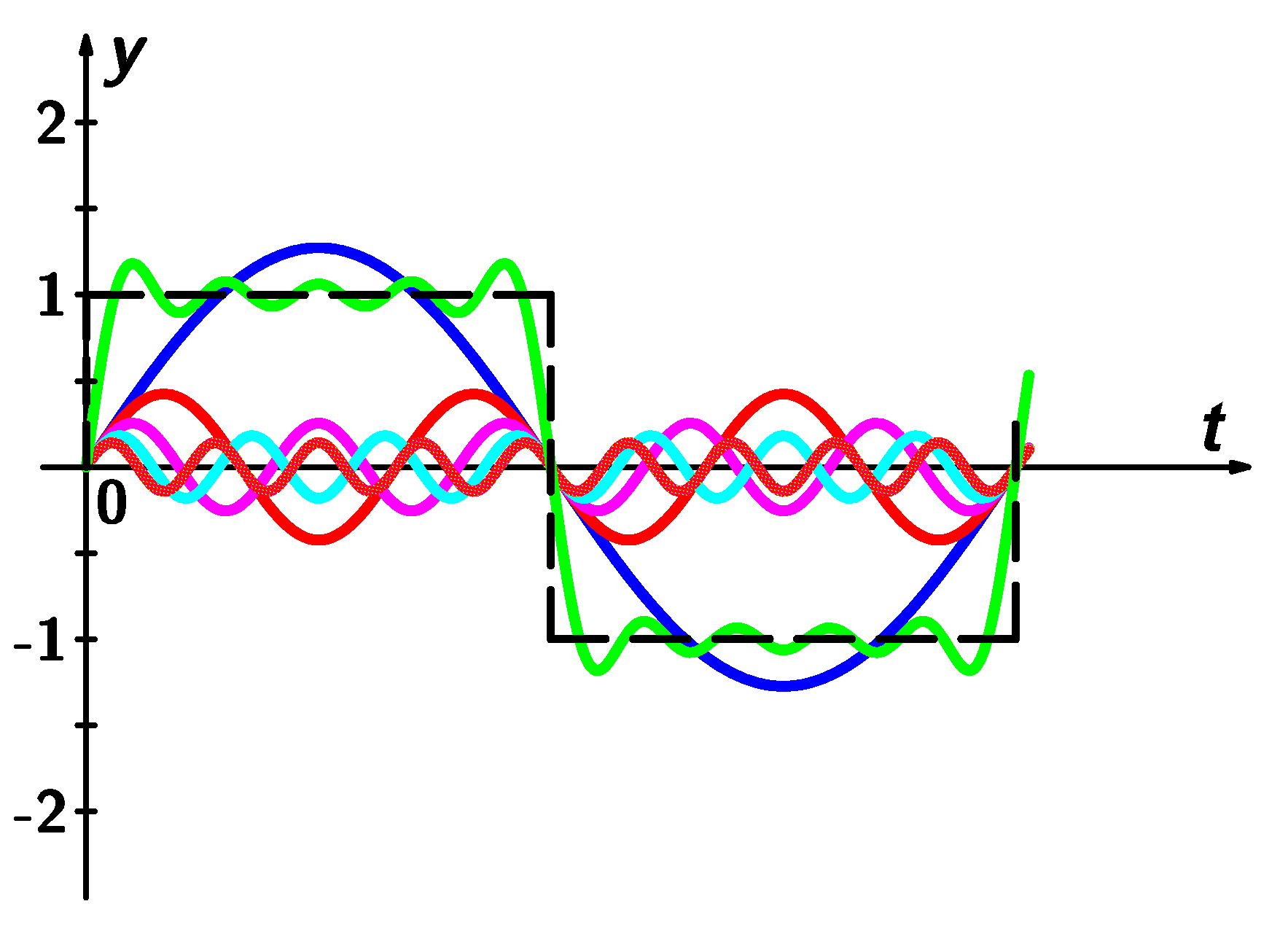
Př. Obdélníkový kmit - viz níže uvedený obrázek.

Fourierovy koeficienty mají tvar:

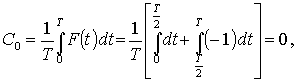
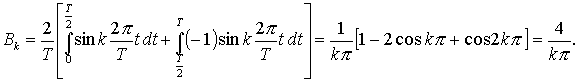
Výše uvedený vztah B_k platí pro k liché, pro k sudé nabývají tyto koeficienty nulových hodnot.
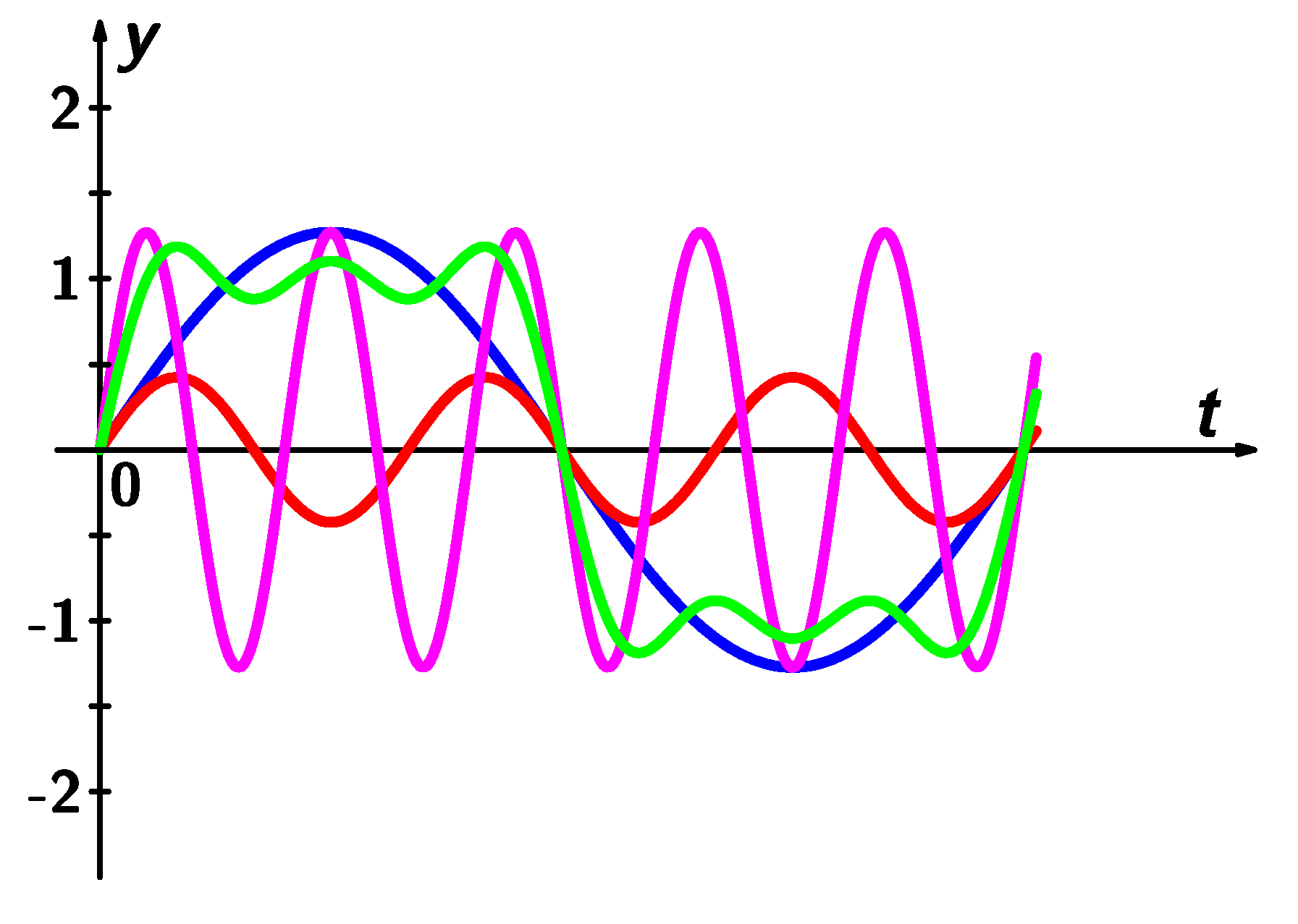
Prvních pět členů Fou rierova rozvoje pro obdélníkový kmit bude mít tvar:

Graf je zobrazen níže.