S pojmem parciální derivace se můžeme setkat, řešíme-li úlohy, kde se používají funkce více proměnných. Vezměme např. funkci

kde x  a y jsou nezávisle proměnné a u = u(x,y) je závisle proměnná veličina. Funkci u(x,y) je možno derivovat buď podle proměnné x nebo podle proměnné y. Postup derivace a jejího značení je uveden níže:

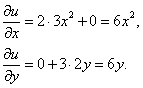
Jestliže derivujeme podle x, považujeme při tom veličinu y za konstantní a naopak, když derivujeme podle y, považujeme veličinu x za konstantu.

     Máme-li funkci u(x,y) dvou proměnných, můžeme se kromě druhých derivací

setkat také s derivacemi

Význam výše uvedených derivací je uveden níže

První výše uvedený výraz dostaneme tak, že funkci u(x, y) zderivujeme nejprve podle proměnné x (přičemž y považujeme za konstantu) a obdržený výsledek potom zderivujeme podle y (přičemž považujeme x za konstantu).

Příklad:  Určete všechny možné parciální derivace funkce u = x² y + x³ y² .

Řešení: Jedná se o derivaci součtu a proto derivujeme každý člen součtu zvlášť.

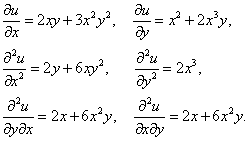
^{V případě smíšených parciálních derivací jsme dostali stejný výsledek, ale toto nemusí platit obecně.}

        ^{S parciálními derivacemi se můžeme ve fyzice nejčastěji setkat především při řešení fyzikálních polí. Je to proto, že veličiny, které popisují pole (intenzita, potenciál) jsouv obecném případě  funkcemi souřadnic a času.}