Sklon křivky. Tečna křivky. Normála.

     Pod sklonem křivky v jejím daném bodě rozumíme směrnici tečny, vedené ke křivce v tomto bodě.

Abychom uměli určit sklon křivky, je třeba umět stanovit pro danou rovnici y = f(x) a souřadnice x, y daného bodu směrnici tečny vedené ke křivce v bodě [x, y]. Ale co je to vlastně tečna křivky?      V elementární geometrii se definuje tečna kružnice jako přímka, která má s kružnicí jen jeden společný bod. Avšak tato definice má smysl jen v případě kružnice. Jestliže se však pokusíme použít této definice pro tečnu paraboly y = x2 , potom by v počátku souřadnic O obě souřadnicové osy vyhovovaly této definici. Je ale jasné, že ve skutečnosti jen osa x je tečnou paraboly v počátku souřadnic. Proto uvedenou definici tečny ke kružnici nelze použít v případě jiných křivek a je nutno stanovit obecnější definici tečny.

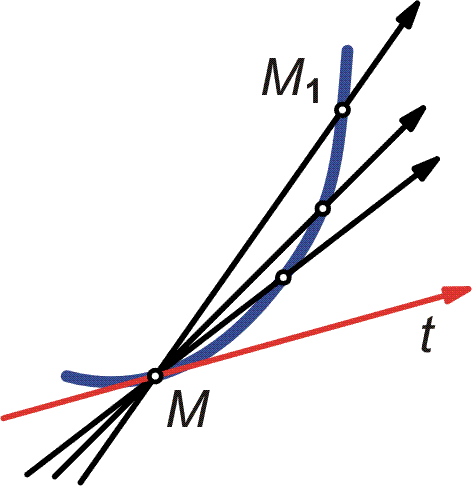     Abychom stanovili tečnu v bodě M k dané křivce, budeme postupovat takto: mimo bod M si na křivce zvolíme ještě bod M₁ (viz obr. vpravo), různý od bodu M a určíme sečnu MM₁. Bude-li se bod M₁ pohybovat po křivce, pak se bude sečna MM₁ otáčet kolem bodu M (viz obr.). 

     Tečnou křivky v bodě M bude limitní poloha MT sečny MM₁ (pokud taková poloha existuje), když bod M₁, který se pohybuje po křivce se blíží bodu M.

Je-li křivka určena rovnicí y = f(x), potom k nalezení její tečny v bodě M = [x, y] stačí znát směrnici této tečny. Zkusme nyní nalézt směrnici tečny ke křivce v bodě M.      Zvětšíme-li souřadnici x bodu M o přírůstek Δx, přejdeme tak k bodu M1 se souřadnicemi x + Δx, y + Δy = = f(x + Δx) (viz obr.). Směrnici tečny MM1, která je rovna tg α, určíme z pravoúhlého trojúhelníka MNM1. Jeho odvěsna MN má velikost přírůstku Δx souřadnice x bodu M a odvěsna NM1 je odpovídajícím přírůstkem souřadnice y: To znamená, že

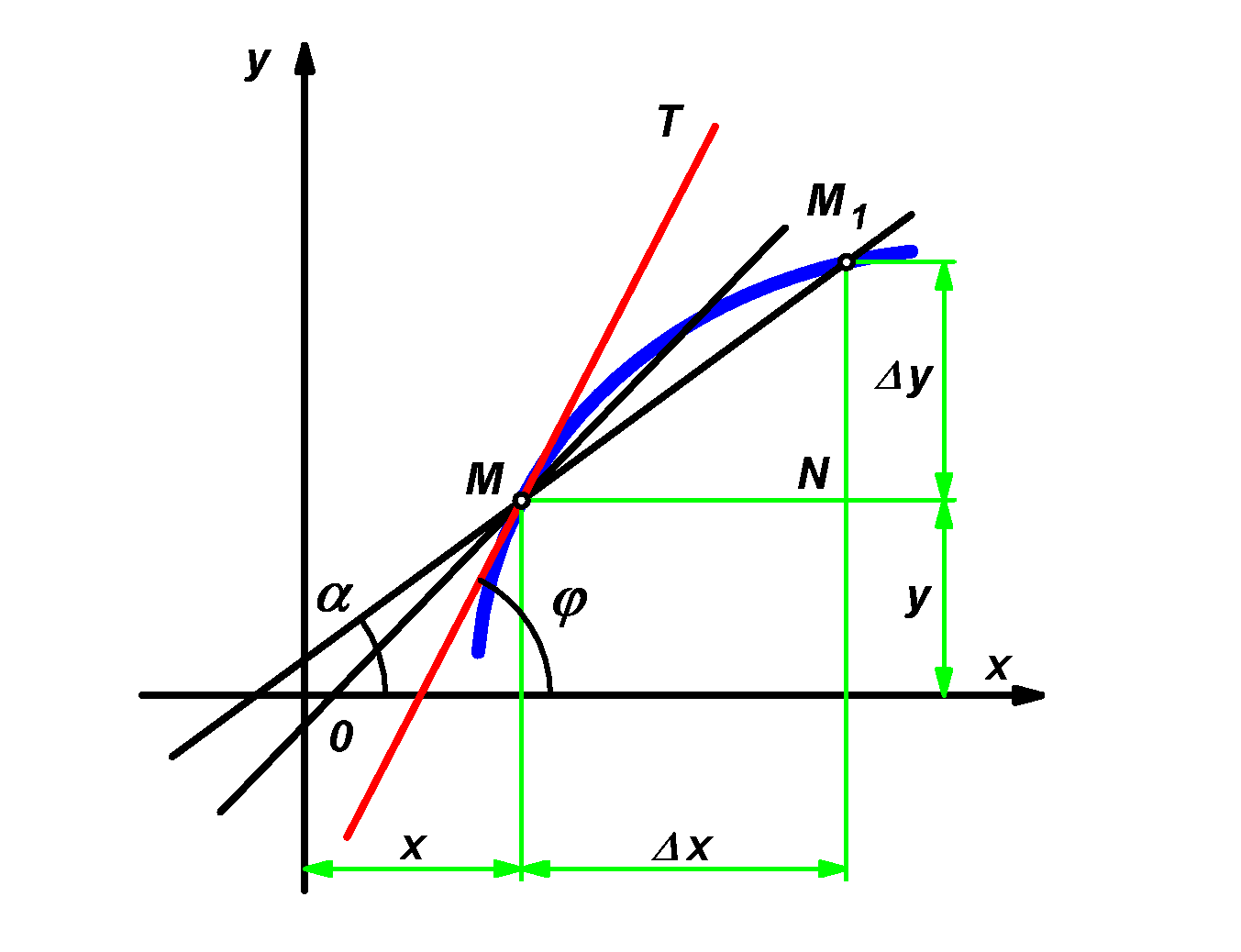     Bude-li se bod M₁ pohybovat po křivce k bodu N, potom přírůstek Δx se bude blížit k nule. Proto je třeba při hledání směrnice tečny nalézt limitu podílu Δy/Δx pro Δx → 0. Označíme-li φ odchylku, kterou svírá tečna s osou x, dojdeme k výsledku:

     Protože

     je derivací  y´= f ´(x) funkce y = f(x) pro hodnotu x rovnou souřadnici x bodu M, můžete učinit tento závěr:

Směrnice tečny křivky , určené rovnicí y = f(x) v bodě křivky M = [x, y], je určena hodnotou derivace y´ = f ´(x) funkce y = f(x) (jejímž grafem je křivka) pro x rovné souřadnici x bodu M.

Jinými slovy: směrnice (tg φ) tečny je derivací souřadnice y = f(x) podle souřadnice x.

     Nyní odvodíme obecné vyjádření rovnice tečny křivky, určené rovnicí y = f(x) v bodě o souřadnicích x₀, y₀ = f(x₀).

Rovnici tečny jako přímky procházející bodem [x₀, y₀] napíšeme ve tvaru

kde k je směrnice tečny. Na základě geometrického významu derivace je k = f ´(x₀). Rovnici tečny je tedy možno napsat v konečném tvaru takto:

Příklad:

     Určete směrnici tečny křivky  y = x³  v bodě o souřadnicích [2, 8].

Řešení:

     Nejprve je nutno určit derivaci funkce y = x³. Proveďte sami (postup řešení pak naleznete zde). Dostaneme vztah y´= 3x². Nyní dosadíme do obecného vyjádření derivace za x = 2, a tím dostaneme

Normála křivky

     Je přímka, která je kolmá k tečně a prochází dotykovým bodem tečny.

Vzhledem k podmínce kolmosti tečny a normály je směrnice normály rovna:

Proto má rovnice normály tvar:

čili

Poznámka:

     Toto ovšem platí za předpokladu, je-li f´(x₀) ≠ 0. V případě f´(x) = 0 je tečna rovnoběžná s osou x, normála je tudíž rovnoběžná s osou y a má tedy rovnici x = x₀. K tomuto závěru je rovněž možno dospět použitím druhé rovnice pro popis normály.

[Zpět na stránku pojem derivace]      [Derivace elementárních funkcí]